目前挑战葛立恒数的有赢的吗？

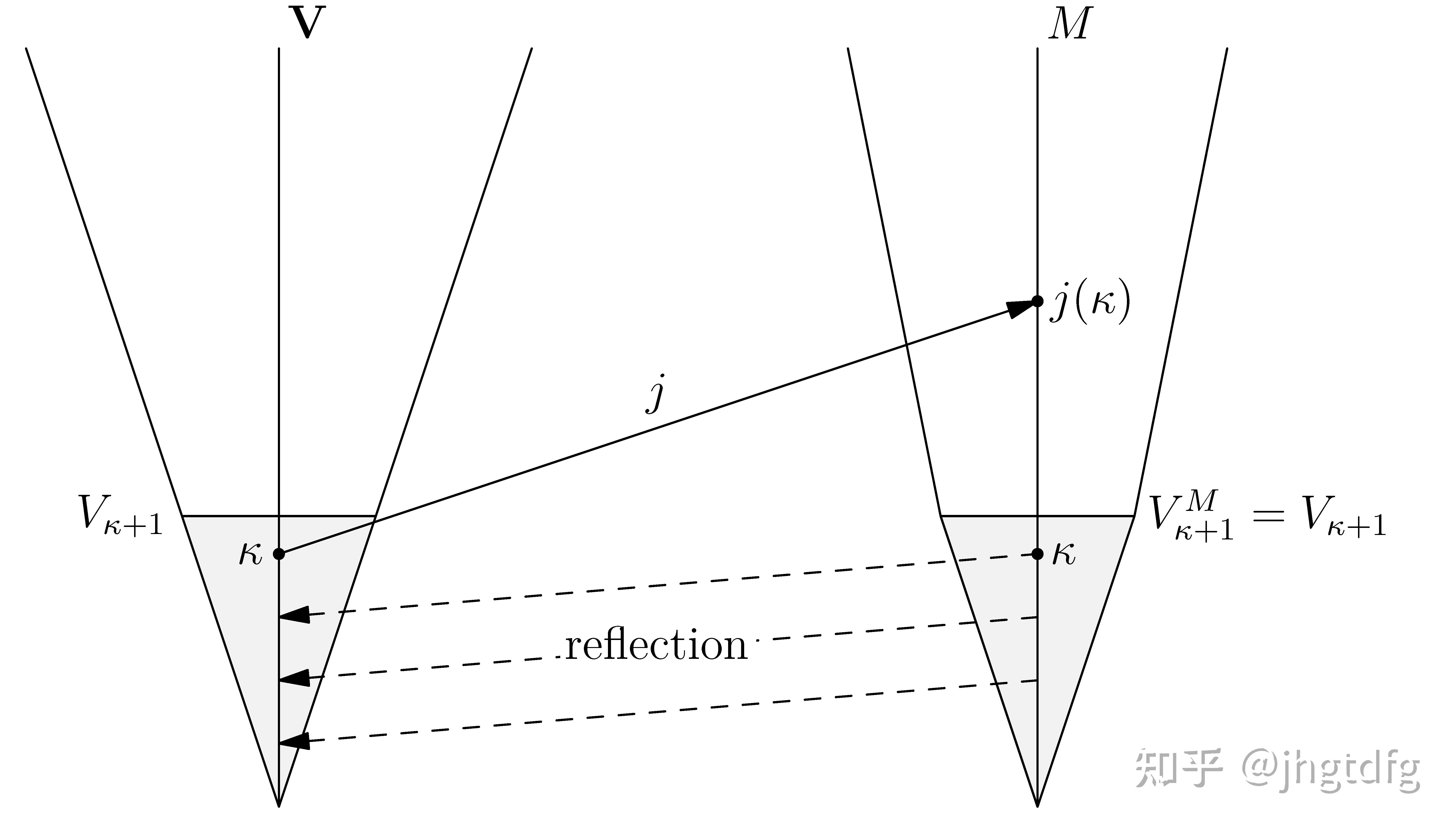
999999^999999^9999999^999999^999999^999999^999999^999999^999999^999999^999999^999999^999999^999999^999999^999999^999999^999999^999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^999999^9999999^999999^999999^999999^k(k定义为非平凡初等嵌入V→M的最小关键点)和葛立恒数比，谁大？

好吧，以上只是在搞笑而已，其实超过葛立恒数还是很简单的，弱一点的方法有用阿克曼函数套娃，康威链式箭头，强一点的则有古德斯坦序列，燃烧数

我随便写的东西居然破百赞了？
那好，我给大家科普一下，其实非平凡初等嵌入V→M的关键点就是现在集合论中大名鼎鼎的可测基数。它还有一个等价的定义，称基数k为可测基数，当且仅当k上存在k完全的非主超滤（所谓滤是大子集的族，按照定义，一个滤的元素有这个集合本身，但没有空集，任意两个元素之交都在这个滤中，同时如果集合的一个子集在这个滤中，那包含这个子集的子集也会在这个滤中。如果集合S上的滤U满足对任意X⊆S，或者X∈U或者S-X∈U，则称之为超滤，如果一个滤由包含同一个非空子集的所有子集构成，则称之为主滤。非主超滤就是说这个滤是超滤，但并不是主滤，而k完全则是说从滤中任意取出几个子集，如果子集的个数少于k，则它们的交也在这个滤中）